Table of Contents
# Matt Watkins for the CP2K-UK summer school 2016 # # heavily lifted from Marcella Iannuzzi's previous presentations, e.g # https://www.cp2k.org/_media/events:2015_cecam_tutorial:iannuzzi_gpw_gapw_b.pdf # # Matt Watkins # School of Mathematics and Physics, University of Lincoln, UK
GPW (GAPW) electronic structure calculations
DFT
Why DFT?
- Explicit inclusion of electronic structure
- predictable accuracy (at least when benchmarked for related systems)
- many observables available (spectroscopy)
- cheaper (better scaling) than many wavefunction based approaches
- ab initio molecular dynamics / Monte Carlo
Hohenberg-Kohn Theorems
Theorem 1
- the potential and hence the total energy are a unique functional of the electronic density, $n(\mathbf{r})$
$$n(\mathbf{r}) \leftrightarrow V_{ext}(\mathbf{r},\mathbf{R})$$
Theorem 2
- the total energy is variational
$$E[n] \geq E[n_{GS}]$$
the energy has several components:
$E_{tot}[n] = E_{kin}[n] + E_{ext}[n] + E_{H}[n] + E_{XC}[n]$
- $E_{kin}$ - kinetic energy of electrons
- $E_{ext}$ - energy due to external potential (pseudo potentials, external bias or electric fields … )
- $E_{H}$ - Hartree energy, classical electrostatic interactions
- $E_{xc}$ - non-classical Coulomb energy: electron correlation
Kohn-Sham: non-interacting electrons
We map the problem of interacting electrons onto an equivalent one with non-interacting electrons with an altered external potential (xc).
We expand the density as a sum of one electron orbital contributions
Electronic density
$$ n(\mathbf{r}) = \sum_i f_i \mid \psi_i (\mathbf{r}) \mid ^2 $$
where $f_i$ is the occupation number of the $i$th orbital
Kinetic energy of non-interacting electrons
$$ T_s[n] = \sum_i f_i \big{<} \psi_i (\mathbf{r}) \mid -\frac{1}{2} \nabla^2 \mid \psi_i (\mathbf{r}) \big{>} $$
Electronic interaction with the external potential
$$ E_{ext} [n] = \int_r n(\mathbf{r}) V_{ext} (\mathbf{r}) \text{d}\mathbf{r}, V_{ext} = \sum_I -\frac{Z_I}{\mid \mathbf{r} - \mathbf{R}_I \mid} $$
with the exact solution as a Slater determinant of the lowest $N$ orbitals
$$ \Psi = \frac{1}{\sqrt{N!}} \text{det} [\psi_1 \psi_2 \psi_3 \cdots \psi_N] $$
KS equations
Using the 2nd Hohenberg-Kohn theorem, we find the electron density that minimises the energy of the system.
But, like in Hartree-Fock theory, we have to ensure that the electron orbitals are orthonormal to prevent the system imploding.
Orthogonality constraint
$$ \Omega_{KS} [\psi_i] = E_{KS}[n] - \sum_{ij} \epsilon_{ij} \int \psi_i^*(\mathbf{r})\psi_j(\mathbf{r})\text{d} \mathbf{r} $$
Variational search in the space of the orbitals
We correct the non-interacting electron model by adding in an (in principle unknown) XC potential that accounts for all quantum mechanical many-body interactions (electron-electron repulsion)
Classical election-electron repulsion
$$ J[n] = \frac{1}{2} \int_r \text{d} \mathbf{r} \int_{r'} \text{d} \mathbf{r'} \frac{n(\mathbf{r})n(\mathbf{r'})}{\mid \mathbf{r} - \mathbf{r'}} = \frac{1}{2} \int_r n(\mathbf{r}) V_H(\mathbf{r}) \text{d} \mathbf{r} $$
Kohn-Sham functional
$$ E_{KS}[n] = T_s[n] + E_{ext}[n] + J[n] + E_{XC}[n] $$
$$ E_{XC}[n] = E_{kin}[n] - T_s[n] + E_{ee}[n] - J[n] $$
The exact functional form for the electron-electron repulsion is not known, but various levels of approximation are available (Jacob's Ladder).
The existence of this functional is guaranteed by the 1st Hohenberg-Kohn Theroem.
This maps mathematically onto the familiar Hartree-Fock model of electronic structure.
KS equations
$$ H_{KS} \psi_i = \big{[} -\frac{1}{2} \nabla^2 + V_{KS} \big{]} \psi_i = \sum_{ij} \epsilon_{ij} \psi_j $$
We can transform the generalised eigenvalue problem given by the KS equations above, to get rid of the nasty sum on the right hand side. In this case $\epsilon_{ij}$ is diagonal, and we get an eigenvalue problem:
$$\big{[} -\frac{1}{2} \nabla^2 + V_{KS} \big{]} \psi_i = \epsilon_i \psi_i$$
- KS equations look like the Schr$\ddot{o}$dinger equations - coupled and highly non-linear ($V_{KS}$ depends on the orbitals!) - self consistent solution (Self Consistent Field - the $V_{KS}$ is consistent with the orbitals) - KS scheme is, in principle, exact (if we knew the exact $E_{XC}$)
Self-consistency
generate an initial guess, from a superposition of atomic densities (typical PW code) or atomic block diagonal density matrix (CP2K)
- generate a starting density $\Rightarrow n^{0}$
- generate the KS potential $\Rightarrow V_{KS}^{0}$
- solve the KS equations $\Rightarrow \epsilon, \psi$
then repeat until convergence
- calculate the new density $\Rightarrow n^{1}$
- calculate the new KS potential $\Rightarrow V_{KS}^{1}$
- new orbitals and energies $\Rightarrow \epsilon^1, \psi^1$
calculate properties from final density and orbitals
Stopping criteria in CP2K are:
- the largest MO derivative ($\frac{\partial E}{\partial C_{ \alpha i}} $) is smaller than `EPS_SCF` (OT)
- the largest change in the density matrix ($P$) is smaller than `EPS_SCF` (traditional diagonalization).
Basis Set Representation(s)
to actually do calculations we need to expand the KS equations into a basis. In CP2K we use Gaussian functions as the primary basis set:
the KS orbitals are then represented as
$$ \psi_i (\mathbf{r}) = \sum_{\alpha} C_{\alpha i} \phi_{\alpha} (\mathbf{r}) $$
the density as
$$ n (\mathbf{r}) = \sum_i \sum_{\alpha \beta} f_i C_{\alpha i} C_{\beta i} \phi_{\alpha} (\mathbf{r})\phi_{\beta} (\mathbf{r}) = P_{\alpha \beta} \phi_{\alpha} (\mathbf{r})\phi_{\beta} (\mathbf{r}) $$
where the density matrix $\mathbf{P}$ is defined.
There is a complication - the basis functions are not orthogonal. We have an *overlap matrix*, $\mathbf{S}$,
$$ S_{\alpha \beta} = \int_r \phi_{\alpha} (\mathbf{r})\phi_{\beta} (\mathbf{r}) \text{d}\mathbf{r} $$
KS total energy
$$ E[\{\psi_i\};\{\mathbf{R}_I\}] = T[\{\psi_i\}] + E_{ext}[n] + E_H [n] + E_{XC}[n] + E_{II} $$
for local of semi-local functionals or
$$ E[\{\psi_i\};\{\mathbf{R}_I\}] = T[\{\psi_i\}] + E_{ext}[n] + E_H [n] + E_{XC}[\{\psi_i\}] + E_{II} $$
for hybrid functionals.
Where $E[\{\psi_i\};\{\mathbf{R}_I\}]$ indicates that the energy depends on the (occupied) KS orbitals (which then give a density) and parametrically on all the $I$ nuclear coordinates, $\mathbf{R}_I$.
Matrix formulation of the KS equations
using the variational principle we get
$$ \mathbf{K}(C)\mathbf{C} = \mathbf{T}(C) + \mathbf{V}_{ext}(C) + \mathbf{V}_H(C) + \mathbf{V}_{XC}(C) = \mathbf{SC}\epsilon $$
Algorithmic challenges
- construct the Kohn-Sham matrix
- Hartree potential
- XC potential
- HF/exact exchange
- core/pseudopotential terms
- fast and efficient minimization of the energy functional
- efficient calculation of the density matrix and construction of the Molecular Orbitals ($\mathbf{C}$)
Construction of the KS matrix should be (and is in CP2K) linear scaling (O(N)) in basis set size. CP2K does this using dual basis set (GPW) techniques - coming up.
Minimization / diagonalization is harder - linear scaling routines are available but are only more efficient for large systems and require considerable computational resources.
GPW method in CP2K
after the general discussion of DFT above, what does CP2K do to solve the KS equations efficiently?
What should you know / look out for, to get good use of the code?
Gaussians and Plane Wave method (GPW)
GPW ingredients
As the name suggests, this method uses two different types of functions
- localized Gaussians, centred at atomic positions
- plane waves
The idea of GPW is to use the plane-waves as an auxiliary basis, primarily to construct the Hartree potential.
This leads to linear scaling KS construction for Gaussian Type Orbitals (GTO)
Guassian basis sets (many matrix elements can be done analytically)
we go a bit further than implied above - to be more accurate, we *contract* several Gaussians to form approximate atomic orbitals $$ \phi_{\alpha} (\mathbf{r}) = \sum_m d_{m\alpha}g_m(\mathbf{r}) $$ where a primitive cartesian Gaussian centred at the origin is given by $$ g_m(\mathbf{r}) = x^{m_x}y^{m_y}z^{m_z} e^{-\alpha_m r^2} $$ and $m_x + m_y + m_z = l$, the angular momentum quantum number of the functions.
- Pseudo potentials
- Plane waves auxiliary basis for Coulomb integrals
- Regular grids and FFT for the density
- Sparse matrices (KS and P)
- Efficient screening
Gaussian Basis set
- localised atom-centred GTO basis
$$ \phi_{\alpha} (\mathbf{r}) = \sum_m d_{m\alpha}g_m(\mathbf{r}) $$
- expansion of the density using the density matrix
$$ n (\mathbf{r}) = \sum_{\alpha \beta} P_{\alpha \beta} \phi_{\alpha}^* (\mathbf{r})\phi_{\beta} (\mathbf{r}) $$
- operator matrices are sparse. By neglecting overlap elements smaller than some number indirectly specified by `EPS_DEFAULT`, the Gaussian functions are localized with finite support. This means that $\mathbf{S, H}$ and $\mathbf{P}$ are sparse.
$$ S_{\alpha \beta} = \int_r \phi_{\alpha} (\mathbf{r})\phi_{\beta} (\mathbf{r}) \text{d}\mathbf{r} $$ $$ H_{\alpha \beta} = \int_r \phi_{\alpha} (\mathbf{r}) V_{KS}(\mathbf{r}) \phi_{\beta} (\mathbf{r}) \text{d}\mathbf{r} $$
Data files
Parameter files distributed with CP2K in $CP2K_ROOT/cp2k/data
(testchroot)mattw@localhost:~/progs/cp2k$ ls cp2k/data/ ALL_BASIS_SETS BASIS_MOLOPT DFTB GTH_POTENTIALS NLCC_POTENTIALS nm12_parameters.xml vdW_kernel_table.dat ALL_POTENTIALS BASIS_RI_cc-TZ ECP_POTENTIALS HFX_BASIS POTENTIAL rVV10_kernel_table.dat BASIS_ADMM BASIS_SET EMSL_BASIS_SETS HF_POTENTIALS README t_c_g.dat BASIS_ADMM_MOLOPT BASIS_ZIJLSTRA GTH_BASIS_SETS MM_POTENTIAL dftd3.dat t_sh_p_s_c.dat
contains sets of basis sets (*BASIS_SET*) and pseudopotentials (*POTENTIAL* except MM_POTENTIAL, which is for classical calculations)
Also parameter files for
- screened exact exchange `t_c_g.dat`
- Grimme type dispersion `dftd3.dat`
- non-local dispersion functionals `vdW_kernel_table.dat, rVV10_kernel_table.dat`
Basis set libraries
There are two main types of basis sets supplied with CP2K
- GTH_BASIS_SETS: atomically optimized sets. These were the first shipped with the code and vary systematically in quality from DZ to QZ for lighter elements. Can be very good for molecular systems, but can be very bad for condensed matter systems.
- BASIS_MOLOPT: molcularly optimized basis sets. These cover most elements of the periodic table, but only with fairly good quality DZVP-MOLOPT-SR-GTH. Should be a good starting point for most condensed matter calculations.
The basis set files provide the contraction coefficients ($d_{m \alpha}$) and exponents ($\alpha_m$) of the Gaussian functions.
$$ \phi_{\alpha} (\mathbf{r}) = \sum_m d_{m\alpha}g_m(\mathbf{r}) $$ $$ g_m(\mathbf{r}) = x^{m_x}y^{m_y}z^{m_z} e^{-\alpha_m r^2} $$
Generally the first column is the exponents ($\alpha_m$ above) and the later columns give the $d_{m \alpha}$, each column being a set $\alpha$. Details can be found in the header of the BASIS_MOLOPT file.
N DZVP-MOLOPT-SR-GTH DZVP-MOLOPT-SR-GTH-q5
1
2 0 2 5 2 2 1
7.341988051825 0.113789156500 0.077765588400 -0.053744330400 -0.007627243700 0.033688455200
2.542637110957 0.097294516500 0.108655219900 -0.165752516200 0.015163333100 0.109813343200
0.888574967229 -0.445077422600 -0.374125427100 -0.317365165600 -0.129388247500 0.856542971300
0.333802200435 -0.584142233900 0.024021712400 -0.312039675200 0.554905847400 0.509681657500
0.112012109029 -0.139562383500 0.979415132500 -0.117936008100 1.001020469600 0.047030652200
Here there are Gaussians with five different exponents ( in Bohr$^{-2}$). From these 5 sets of functions are built, two $s$ functions (2nd and 3rd columns), 2 sets of $p$ functions (4th and fifth columns) and one set of $d$ functions (last column).
Note that the contraction coefficients are not varied during calculation. For the nitrogen basis above we have $2 + 2 \times 3 + 1 \times 5 = 13$ variables to optimize for each nitrogen atom in the system.
(CP2K tends to use general contractions for efficiency, allowing maximum use of recursion relations to generate matrix elements for high angular momentum functions).
GTH pseudopotentials
Accurate and transferable with few parameters. Include scalar relativistic effects. Available for all atoms $\in Z_{ion} < 86$
- Norm-conserving, separable, dual-space
- Local PP : short-range and long-range terms
$$ V_{loc}^{PP}(r) = \sum_{i=1}^4 C_i^{PP} (\sqrt{2} \alpha^{PP} r)^{2i-2}e^{-(\alpha^{PP}r)^2} - \frac{Z_{ion}}{r}erf(\alpha^{PP}r) $$
first term in sum is short ranged, and analytically calculated in Gaussian basis. Second term is long ranged, and merged into the electrostatic calculation (see later)
- non-local PP with Gaussian type operators
$$ V_{nl}^{PP}(\mathbf{r},\mathbf{r'}) = \sum_{lm} \sum_{ij} \big{<} \mathbf{r} \mid p_i^{lm} \big{>}h^l_{ij} \big{<} p_j^{lm} \mid \mathbf{r'} \big{>} $$
$$ \big{<} \mathbf{r} \mid p_i^{lm} \big{>} = N_i^l Y^{lm}(\hat{r})r^{l+2i-2}e^{-\frac{1}{2}(\frac{r}{r_l})^2} $$
You can scan through potentials available at here
Original papers: Goedeker, Teter, Hutter, PRB 54 (1996), 1703 and Hartwigsen, Goedeker, Hutter, PRB 58 (1998) 3641
Electrostatics
- long-range term: Non-local Hartree Potential
Poisson equation solved using the auxiliary plane-wave basis $$ E_H[n_{tot}] = \frac{1}{2} \int_r \text{d}\mathbf{r} \int_{r'} \text{d}\mathbf{r'} \frac{n(\mathbf{r})n(\mathbf{r'})}{\mid \mathbf{r} - \mathbf{r'}} $$
where $n_{tot}$ includes the nuclear charge as well as the electronic. (The nuclear charge density is (of course) represented as a Gaussian distribution with parameter $R_I^c$ chosen to cancel a similar term from the local part of the pseudopotential)
- FFT (scaling as $N\text{log}N$) gives
$$\tilde{n}(\mathbf{r}) = \frac{1}{\Omega} \sum_G \tilde{n}(\mathbf{G})e^{i\mathbf{G \cdot r}})$$
In the $G$ space representation the Poisson equation is diagonal and the Hartree energy is easily evaluated
$$ E_H[n_{tot}] = 2 \pi \Omega \sum_G \frac{\tilde{n}(\mathbf{G}) ^* \tilde{n}(\mathbf{G}) }{\mathbf{G}^2} $$
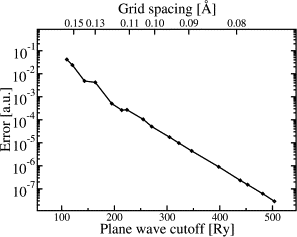
- The electrostatic energy converges rapidly with the grid spacing / planewave cutoff
Real space integration
Finite cutoff and simulation box define a realspace grid
- density collocation
$$ n(\mathbf{r}) = \sum_{\alpha \beta} P_{\alpha \beta} \phi_{\alpha}^* (\mathbf{r})\phi_{\beta} (\mathbf{r}) \rightarrow \sum_{\alpha \beta} P_{\alpha \beta} \bar{\phi}_{\alpha \beta} (\mathbf{r}) = n(\mathbf{R}) $$ where $n(\mathbf{R})$ is the density at grid points in the cell, and $\bar{\phi}_{\alpha \beta}$ are the products of two basis functions.
- numerical approximation of the gradient $n(\mathbf{R}) \rightarrow \nabla n(\mathbf{R})$
- $\epsilon_{xc}$ and derivatives evaluated on the grid
$$v_{XC}[n](\mathbf{r}) \rightarrow V_{XC}(\mathbf{R}) = \frac{\partial \epsilon_{xc}}{\partial n} (\mathbf{R})$$
- real space integration
$$ H_{HXC}^{\mu \nu} = \big{<} \mu \mid V_{H,XC} (\mathbf{r}) \mid \nu \big{>} \rightarrow \sum_R V_{H,XC} (\mathbf{R}) \bar{\phi}_{\alpha \beta} (\mathbf{R}) $$
If you have PRINT_LEVEL MEDIUM you can see at each SCF cycle some details of this process - particularly how many electrons and the core charge mapped onto the grids.
For instance, for CH2O and a CUTOFF of 400 Ry with GTH pseudos Trace(PS): 12.0000000000
Electronic density on regular grids: -11.9999999997 0.0000000003 Core density on regular grids: 11.9999999994 -0.0000000006 Total charge density on r-space grids: -0.0000000003 Total charge density g-space grids: -0.0000000003
The trace of the density matrix gives us the number of (valence) electrons in the system - 12 in this case
- 6 valence $e^-$ for O
- 4 valence $e^-$ for C
- 2 valence $e^-$ for 2H
We see that 11.9999999997 electrons are mapped onto the grids, along with 11.9999999994 nuclear charge. You should aim for at a very minimum accuracy of 10−8. If not, increase the cutoff.
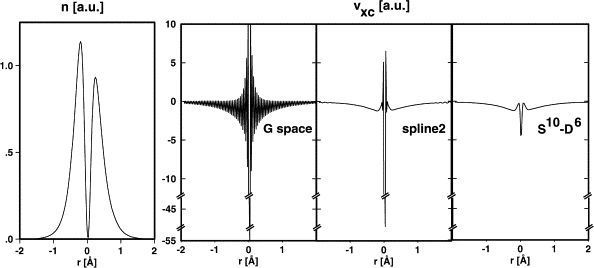
Energy ripples
Low density regions can cause unphysical behaviour of $XC$ terms (such as $\frac{\mid \nabla n \mid ^2}{n^{\alpha}}$)
GTH pseudos have small density at the core - graph of density and $v_{XC}$ through a water molecule. These spikes can cause ripples in the energy as atoms move relative to the grid. These can be very problematic when trying to calculate vibrational frequencies.
There are smoothing routines `&XC_GRID / XC_DERIV`, see the exercise converging_cutoff.
Avoid ripples with higher a cutoff, or GAPW methodology.
Whatever you do don't change settings between simulations you want to compare.
Multigrids
When we want to put (collocate) a Gaussian type function onto the realspace grid, we can gain efficiency by using multiple grids with differing cutoff / spacing.
More diffuse Gaussians can be collocated onto coarser grids
specified in input as:
&MGRID
CUTOFF 400
REL_CUTOFF 60
NGRIDS 5
&END MGRID
you can see in the output
------------------------------------------------------------------------------- ---- MULTIGRID INFO ---- ------------------------------------------------------------------------------- count for grid 1: 24832 cutoff [a.u.] 200.00 count for grid 2: 11934 cutoff [a.u.] 66.67 count for grid 3: 6479 cutoff [a.u.] 22.22 count for grid 4: 1976 cutoff [a.u.] 7.41 count for grid 5: 215 cutoff [a.u.] 2.47 total gridlevel count : 45436
For this system (formaldeyhde with an aug-TZV2P-GTH basis) that 45436 density matrix elements ($\bar{\phi}_{\alpha \beta}$) were mapped onto the grids. To be efficient, all grids should be used.
To fully converge calculations both CUTOFF and REL_CUTOFF need to be increased together otherwise the highest grid may not be used.
Timings
At the end of the run you'll see timings - these can be very useful for understanding performance.
Here we can see the timings for the formaldehyde example. It is in a large box, and the operations on grids dominate the cost on a single processor.
-------------------------------------------------------------------------------
- -
- T I M I N G -
- -
-------------------------------------------------------------------------------
SUBROUTINE CALLS ASD SELF TIME TOTAL TIME
MAXIMUM AVERAGE MAXIMUM AVERAGE MAXIMUM
CP2K 1 1.0 0.013 0.013 24.048 24.048
qs_energies 1 2.0 0.000 0.000 23.417 23.417
scf_env_do_scf 1 3.0 0.000 0.000 22.962 22.962
scf_env_do_scf_inner_loop 14 4.0 0.001 0.001 22.962 22.962
qs_ks_update_qs_env 14 5.0 0.000 0.000 19.555 19.555
rebuild_ks_matrix 14 6.0 0.000 0.000 19.554 19.554
qs_ks_build_kohn_sham_matrix 14 7.0 0.002 0.002 19.554 19.554
qs_vxc_create 14 8.0 0.000 0.000 8.977 8.977
xc_vxc_pw_create 14 9.0 0.273 0.273 8.977 8.977
xc_rho_set_and_dset_create 14 10.0 0.086 0.086 8.147 8.147
pw_transfer 203 9.2 0.009 0.009 7.539 7.539
fft_wrap_pw1pw2 203 10.2 0.001 0.001 7.530 7.530
pw_poisson_solve 14 8.0 0.458 0.458 7.457 7.457
xc_functional_eval 14 11.0 0.000 0.000 7.395 7.395
pbe_lda_eval 14 12.0 7.394 7.394 7.394 7.394
fft_wrap_pw1pw2_200 87 10.8 0.400 0.400 7.147 7.147
fft3d_s 204 12.1 4.799 4.799 4.805 4.805
qs_rho_update_rho 15 5.0 0.000 0.000 3.631 3.631
calculate_rho_elec 15 6.0 0.711 0.711 3.631 3.631
ps_wavelet_solve 14 9.0 3.418 3.418 3.496 3.496
density_rs2pw 15 7.0 0.001 0.001 2.882 2.882
sum_up_and_integrate 14 8.0 0.040 0.040 1.917 1.917
integrate_v_rspace 14 9.0 0.378 0.378 1.877 1.877
potential_pw2rs 14 10.0 0.005 0.005 1.498 1.498
pw_gather_s 104 11.5 1.274 1.274 1.274 1.274
pw_scatter_s 99 12.8 1.028 1.028 1.028 1.028
pw_nn_compose_r 84 10.5 0.968 0.968 0.968 0.968
pw_poisson_rebuild 14 9.0 0.000 0.000 0.897 0.897
ps_wavelet_create 1 10.0 0.000 0.000 0.897 0.897
RS_z_slice_distribution 1 11.0 0.897 0.897 0.897 0.897
qs_init_subsys 1 2.0 0.001 0.001 0.567 0.567
qs_env_setup 1 3.0 0.000 0.000 0.563 0.563
qs_env_rebuild_pw_env 2 3.5 0.000 0.000 0.563 0.563
pw_env_rebuild 1 5.0 0.000 0.000 0.563 0.563
pw_grid_setup 5 6.0 0.000 0.000 0.516 0.516
pw_grid_setup_internal 5 7.0 0.012 0.012 0.516 0.516
-------------------------------------------------------------------------------
Warnings
Also check if you get an output like
The number of warnings for this run is : 0
if there are warnings, you should try and understand why!