Kinetic Monte Carlo simulations for the diffusion of molecules on a substrate

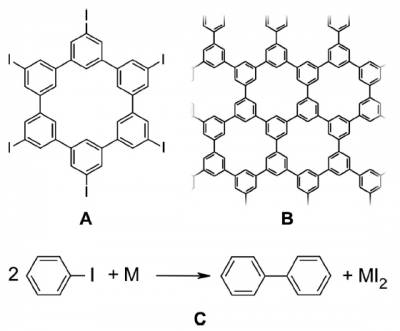
The molecule shown in the image (hexaiodo-substituted macrocycle cyclohexa-m-phenylene (CHP) ), when deposited on a noble metal substrate such as Cu(111) , Ag(111) or Au(111), at room temperature looses the I atoms and starts diffusing.

The relative probability of diffusion and of binding to a neighboring molecule determine the shape of the network that will be obtained. The experiments performed at Empa [ http://dx.doi.org/10.1021/ja107947z J. AM. CHEM. SOC. 2010, 132, 16669–16676 ] shows that on a Cu substrate dendrites will form while on a Au substrate 2D networks will form.

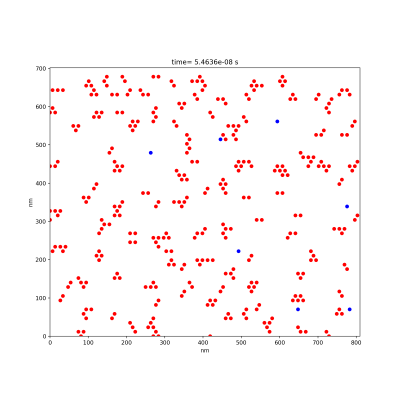
The python program KMC.py will allow you to simulate the diffusion and binding of molecules once the energy barriers for the diffusion event and for the binding event as well as the simulation temperature will be defined.

During the execution the program shows snapshots of the positions of the molecules.

Molecules free to diffuse will be represented via blue dots. Molecules that irreversibly formed a bond with a neighboring molecule will be represented by red dots. At the end of the execution a snapshot of the final configuration of the system is saved an image file. The program asks you for some input:

 
coverage
update graph each steps
temperature in K
diffusion barrier
binding barrier

TASK 1 execute the program with the following parameters:

coverage 0.1
update graph each steps 500
number of steps 100000
temperature in K 300
diffusion barrier 0.1
binding barrier 0.1

Observe how events occur. Observe how time evolves. Did the job perform all the 100000 steps? Why? Observe the patterns obtained.

TASK 2 execute the program with the following parameters:

coverage 0.1
update graph each steps 500
number of steps 100000
temperature in K 300
diffusion barrier 0.3
binding barrier 0.4

Do you notice differences in the way events occur? How is evolving time compared to the previous case? How does the final geometry differ form the previous case?

Now have a look at the python code. The MAIN section

#### MAIN KMC LOOP
t=0

#### at the beginning we have to check possible events for all molecules
tobeupdated=[iu for iu in range(len(molecules))]
possible_events=[]
for i in range(nsteps):
    #### check possible events for selected set of molecules
    possible_events=possible_events+events(molecules,tobeupdated,nx,ny)

    if possible_events==[]:
       print "no more events possible"
       break
    #### compute total rate (can be imporved)
    R=total_rate(possible_events,rates)

    #### decide which event to apply 
    selected_event=find_event(R,rates,possible_events)

    #### apply the event end update partially the list of events
    possible_events,tobeupdated=apply_event(molecules,selected_event,possible_events)

    #### update time
    rho2=np.random.random()
    dt=-np.log(rho2)/R
    t=t+dt

is very simple and reflects the basic steps of the KMC approach. On the contrary, the function needed to create the list of events is quite complex:

def events(m,selection,nx,ny):
    allevents=[]
    set=[]
    #### list of first neighbors (relative position)
    set.append([[0,0,1,0],[1,0,0,0],[0,1,1,0],[-1,1,1,0],[-1,0,0,0],[-1,0,1,0]])
    set.append([[1,-1,-1,0],[1,0,0,0],[1,0,-1,0],[0,0,-1,0],[-1,0,0,0],[0,-1,-1,0]])

    for i in selection:
        le=[]
        #### consider only molecules that are not binded
.
.
.

TASK 3 Have a look on the section of the code that create the list of events, comment on which are the critical points in setting up a KMC simulation to describe a real process.

TASK 4 At each step of the simulaiton the list of possible events is created (or, betetr, updated) an event is chosen randomly and is then actuated. Would it be possible to execute simultaneously more events at each KMC step?