Geometry Optimization
Introduction
Geometry optimization is a process of changing the system's geometry (the nuclear coordinates and potentially the lattice vectors) to minimize the total energy of the systems.
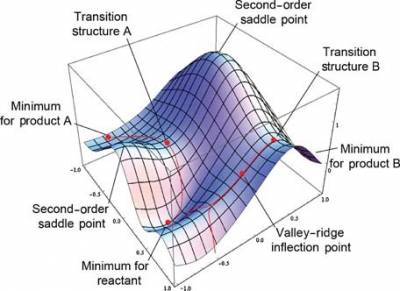
Potential energy surface describes the energy of a system, especially a collection of atoms, in terms of certain parameters, normally the positions of the atoms.
Consider a potential energy surface (PES) as below, the goal is to find the global (or local) minimum, such as the minimum for reactant or product. The commonly-used algorithms include Conjugate gradient method , Quasi-Newton method and its variant BFGS method.
The BFGS method is more efficient when the initial guess is not far from the minimum.
Mathematically, the minimum should fulfill two requirements:
1. The gradient should be zero, $\frac{dE}{dr} = 0 $
2. The sign of Hessian should be all positive, $\frac{d^2E}{dr^2} > 0 $
Hessian: the second derivative of the energy with respect to geometry, $\frac{d^2E}{dr^2}$
To ensure these requirements, one should perform Vibrational Analysis to examine the eigenvalues of the Hessian. If there are some negative values, it means this point is not the minimum.
Exercises
In this exercise, you will perform geometry optimization using DFT. See GEO_OPT
Note the different RUN_TYPE and the changed PROJECT name. The latter is not strictly necessary but recommended since CP2K automatically creates additional files using this project name as a prefix.
- H2O.inp
&GLOBAL PROJECT H2O RUN_TYPE GEO_OPT PRINT_LEVEL MEDIUM &END GLOBAL &MOTION &GEO_OPT MAX_ITER 3000 OPTIMIZER BFGS #Most efficient minimizer, but only for 'small' systems &END GEO_OPT &END MOTION &FORCE_EVAL METHOD Quickstep ! Electronic structure method (DFT,...) &DFT BASIS_SET_FILE_NAME BASIS_MOLOPT POTENTIAL_FILE_NAME POTENTIAL &POISSON ! Solver requested for non periodic calculations PERIODIC NONE PSOLVER WAVELET ! Type of solver &END POISSON &SCF ! Parameters controlling the convergence of the scf. This section should not be changed. SCF_GUESS ATOMIC EPS_SCF 1.0E-6 MAX_SCF 300 &END SCF &XC ! Parameters needed to compute the electronic exchange potential &XC_FUNCTIONAL PBE &END XC_FUNCTIONAL &END XC &END DFT &SUBSYS &CELL ABC 10 10 10 PERIODIC NONE ! Non periodic calculations. That's why the POISSON section is needed &END CELL &TOPOLOGY ! Section used to center the atomic coordinates in the given box. Useful for big molecules &CENTER_COORDINATES &END COORD_FILE_FORMAT xyz COORD_FILE_NAME ./H2O.xyz &END &KIND H ELEMENT H BASIS_SET DZVP-MOLOPT-GTH POTENTIAL GTH-PBE-q1 &END KIND &KIND O ELEMENT C BASIS_SET DZVP-MOLOPT-GTH POTENTIAL GTH-PBE-q6 &END KIND &END SUBSYS &END FORCE_EVAL
- H2O.xyz
3 Water O 5 5.00000 5.11779 H 5 5.75545 4.52884 H 5 4.24455 4.52884
You can also directly open an XYZ file in VMD to visualize it:
$ vmd H2O.xyz
After running this, you will have the following files:
$ ls H2O* H2O-1.restart H2O-1.restart.bak-3 H2O.out H2O-RESTART.wfn.bak-1 H2O-1.restart.bak-1 H2O-BFGS.Hessian H2O-pos-1.xyz H2O-RESTART.wfn.bak-2 H2O-1.restart.bak-2 H2O.inp H2O-RESTART.wfn H2O-RESTART.wfn.bak-3
Take a look at the output file, especially the following section (repeated the number of cycles it took to reach convergence):
-------- Informations at step = 1 ------------ Optimization Method = BFGS Total Energy = -14.9417142787 Real energy change = -0.1955604816 Predicted change in energy = -0.1885432833 Scaling factor = 0.0000000000 Step size = 0.2677976891 Trust radius = 0.4724315332 Decrease in energy = YES Used time = 19.018 Convergence check : Max. step size = 0.2677976891 Conv. limit for step size = 0.0030000000 Convergence in step size = NO RMS step size = 0.1458070233 Conv. limit for RMS step = 0.0015000000 Convergence in RMS step = NO Max. gradient = 0.0287243359 Conv. limit for gradients = 0.0004500000 Conv. for gradients = NO RMS gradient = 0.0180771987 Conv. limit for RMS grad. = 0.0003000000 Conv. for gradients = NO ---------------------------------------------------
For each convergence criterion, you see the value which is used to check whether convergence is reached and convergence is only reached if all of them are satisfied simultaneously.
Applications
Geometry optimization has been widely used in surface science and computational catalysis. Based on electronic structure theory or force fields, the structures are optimized under 0 K to calculate the potential energy. To obtain the Gibbs free energy, one can use $G = E_{DFT} + ZPE - TS$, where the latter two terms can be estimated by the Vibrational Analysis .
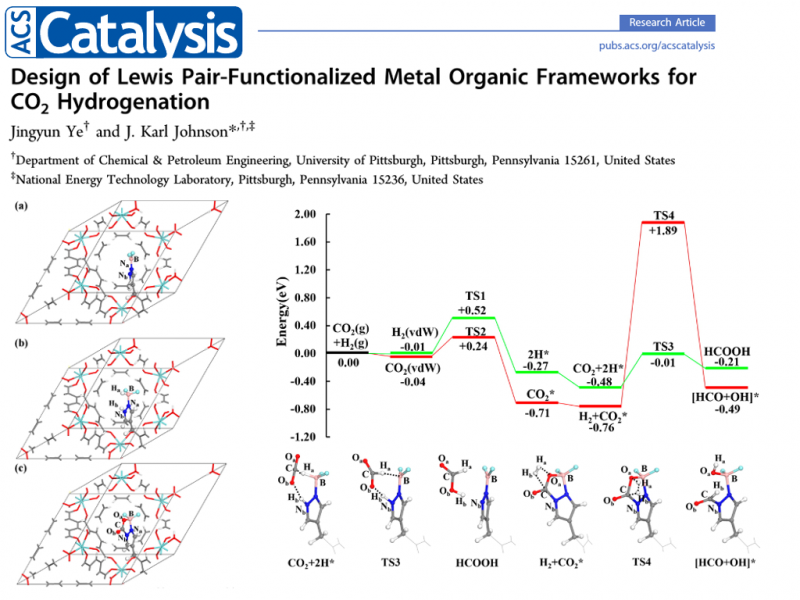Jingyun Ye & J. Karl Johnson; 2015; Design of Lewis Pair-Functionalized Metal
Organic Frameworks for CO2 Hydrogenation
ACS Catal. 5: 2921−2928