Provide a freely available computer code to perform accurate and efficient DFT calculations on large, complex systems such as e.g. liquids, crystals, proteins and interfaces. Both static property calculations (such as spectra computed with TDDFT or as derivative properties of the total energy) and dynamical properties (e.g. diffusion, based on molecular dynamics) are possible.

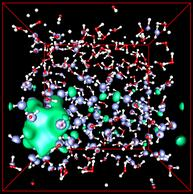
Shown on the left is a representation of the lowest unoccupied molecular orbital (LUMO) of a sample 256 water molecules (see also our picture gallery).

Quickstep is a part of CP2K.

The following is an incomplete list of the methods that provide the core of the Quickstep (QS) code. More complete information can be found in the references.

Quickstep is based on the Gaussian and plane waves method (GPW) and its augmented extension (GAPW). Central in this approach is a dual basis of atom centred Gaussian orbitals and plane waves (regular grids). The former is used to represent the wave functions and e.g. the Kohn-Sham matrix, whereas the latter is used to represent the electronic density. The key advantages are:

• A compact representation of the wave function, only relatively few basis functions per atom are needed as compared to plane wave representations. This allows for memory friendly and efficient algorithms.

• The matrix representation of the Kohn-Sham matrix and density matrix become sparse with increasing system size, allowing for linear scaling methods to perform the density matrix optimisation.

• Linear scaling computation of the Kohn-Sham energy and matrix is readily achieved using screening techniques and Fast Fourier Transforms to compute the Hartree energy.

The orbital transformation (OT) method is a direct minimisation scheme that allows for efficient wave function optimisation. It is, especially for large systems and large basis sets, significantly faster than diagonalisation/DIIS based methods, and is guaranteed to converge. Even though it scales cubically with system size, approx. 1000 atoms (20k-30k basis functions) can be studied fairly easily.

Ab initio molecular dynamics simulations based on the Born-Oppenheimer approach can be performed and are made efficient using a density matrix extrapolation scheme.

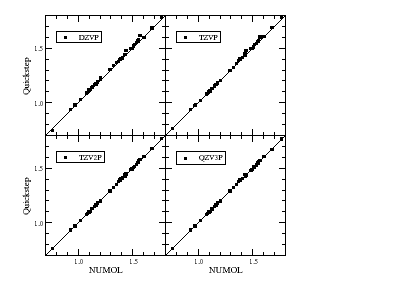
Maintaining good accuracy throughout is an important target, and a sequence of systematically improving basis sets for use with the Goedecker-Teter-Hutter pseudopotentials has been constructed. The picture on the left shows that nearly perfect agreement with a fully converged benchmark method (NUMOL) can be obtained.

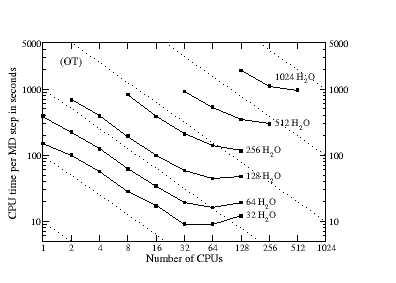Good efficiency can be obtained both in serial and in parallel on a wide range of architectures, including common desktop PCs. Shown on the left is are benchmark calculations on a Power4+ parallel supercomputer, where the time per MD step is shown for samples of liquid water (PBC) with a TZV2P basis set (a maximum of approx. 40000 basis functions) using high quality convergence settings. The dashed lines indicate ideal scaling.

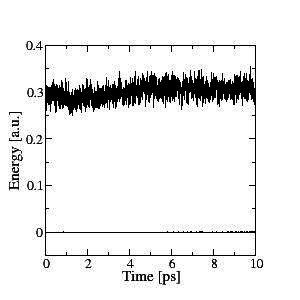
Stable Born-Oppenheimer molecular dynamics can be performed efficiently, and a good conservation of the constant of motion is obtained. This is shown on the left for a 10ps NVE simulation of a sample of 64 water molecules at room temperature. The upper line is the ionic kinetic energy and the lower line is the constant of motion (total energy).

More soon …

Just nice pictures of systems that have been treated with Quickstep.

• CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations, T. D. Kühne et al. J. Chem. Phys. 152, 194103 (2020)

• Quickstep: fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comp. Phys. Comm. 167, 103 (2005).

• Quickstep: Make the atoms dance, M. Krack and M. Parrinello, Forschungszentrum Jülich, NIC Series, Vol. 25, 29 (2004).

• An efficient orbital transformation method for electronic structure calculations, J. VandeVondele and J. Hutter, J. Chem. Phys. 118, 4365 (2003).

• All-electron ab-initio molecular dynamics, M. Krack and M. Parrinello, Phys. Chem. Chem. Phys. 2, 2105 (2000).

• The Gaussian and augmented-plane-wave density functional method for ab initio molecular dynamics simulations, G. Lippert, J. Hutter, and M. Parrinello, Theor. Chem. Acc. 103, 124 (1999).

• A hybrid Gaussian and plane wave density functional scheme, G. Lippert, J. Hutter, and M. Parrinello Mol. Phys. 92, 477 (1997).